Over the past two months, I released three new updates of expltools, the bundle that provides the explcheck static analyzer for the expl3 programming language.

These updates include major improvements but did not yet advance the final stage of the pipeline, flow analysis, which I teased in the previous post. That’s because our work on flow analysis so far has been groundwork: figuring out how to adapt static-analysis techniques to expl3 before moving on to implementation.

In this post, I outline the flow graph structure currently used to represent expl3 code and describe our adaptation of the reaching definitions algorithm for dynamically scoped languages like expl3.

Chunks, edges, and flow graphs

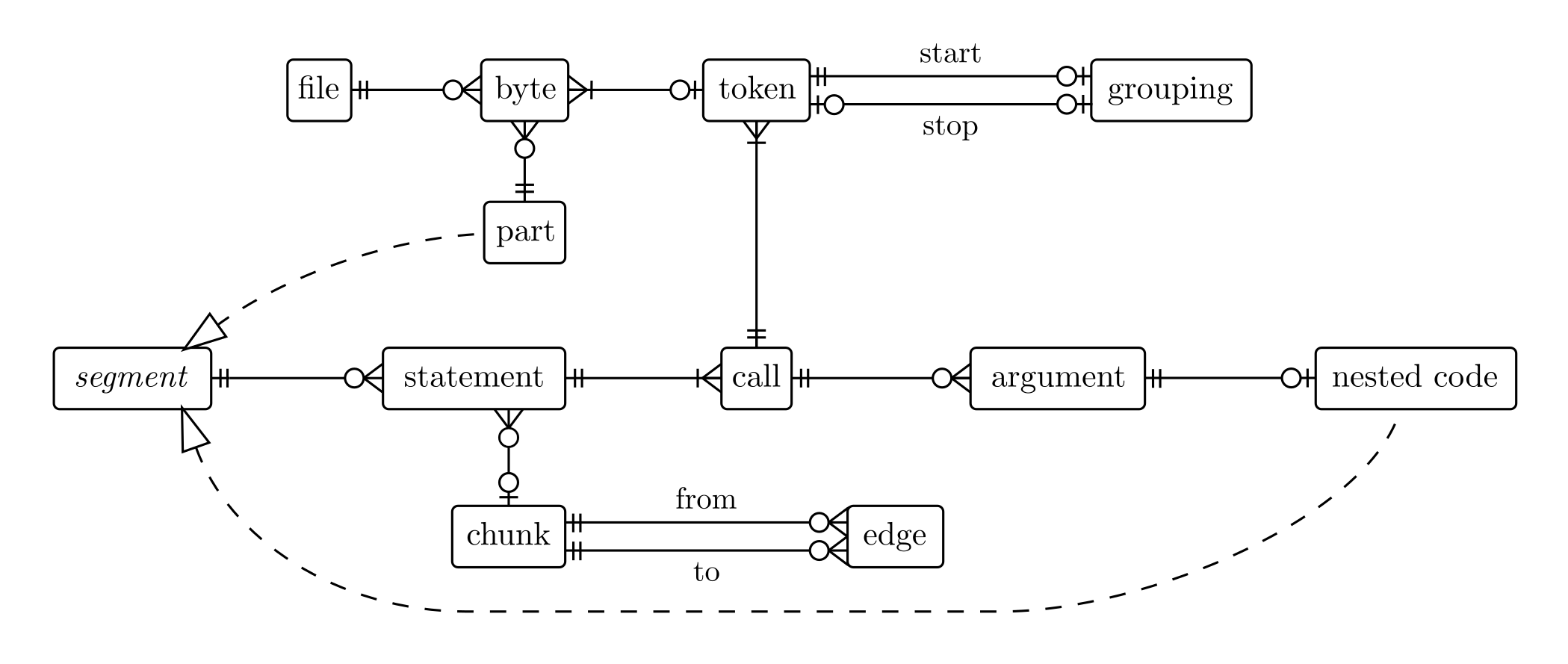
In the previous post, we introduced segments as the units of top-level code in expl3 parts and nested code in T- and F-branches of conditionals, function definitions, and others. Each segment contains zero or more statements found during semantic analysis.

Flow analysis links statements using directed edges to form a flow graph. It also partitions each segment into chunks: sequences of recognized statements separated by OTHER_TOKENS_COMPLEX statements, which contain arbitrary TeX code that may have side effects.

Static edges and confidence

Some edges arise directly from the static structure of an expl3 program. These are known without extra analysis and are called static edges.

Following statements and chunks, conditionals

Within a chunk, statements typically follow one another deterministically. Explcheck does not record these next-statement edges explicitly, but the analysis implicitly assumes them to be present.

The most common explicitly recorded static edge is NEXT_CHUNK, which represents moving to the following chunk. We add NEXT_CHUNK edges as follows:

1. Connect the last statement of each chunk in an expl3 part to the first statement of the first chunk in the next expl3 part.
2. Connect the last statement of each chunk to the first statement of the next chunk in the same segment.

Other common static edges are TF_BRANCH and TF_BRANCH_RETURN:

1. For each conditional function, add a TF_BRANCH edge to the first statements of the first chunks in its T- and F-branches.
2. For each T- and F-branch, add a TF_BRANCH_RETURN edge from the last statement of its last chunk to the statement following its conditional function.

Confidence

All edges come with varying certainty: TeX code between chunks may change the execution state in arbitrary ways, and a conditional function only executes one branch. Edges therefore have a confidence of either MAYBE or DEFINITELY.

For NEXT_CHUNK edges, the confidence is usually MAYBE; it becomes DEFINITELY only between immediately adjacent expl3 parts or between consecutive statements in the same chunk when the first statement has no out-edges.

For TF_BRANCH edges, the confidence is always MAYBE, since we generally do not know which branch will run. For TF_BRANCH_RETURN, the confidence is always DEFINITELY, because once a branch runs, control always returns from it.

Dynamic edges and reaching definitions

Other edges depend on runtime behavior and dynamic scoping. These require estimation and are called dynamic edges.

Function definitions and calls

A key example is function calls and returns: FUNCTION_CALL and FUNCTION_CALL_RETURN. Determining them requires knowing which function definitions may reach each call.

If a function name has only one definition, we might assume that definition is used. But that definition may not reach the call. And often, multiple definitions share the same name, so we must determine which ones are used.

We start by building only the static edges. Then, we run the reaching definitions algorithm. Afterwards, we insert the dynamic edges:

1. For each function call, add a FUNCTION_CALL edge to the first statement of the first chunk in every definition that reaches it.
2. For each definition, add a FUNCTION_CALL_RETURN edge from the last statement of its last chunk to the statement following any call it can reach.

For FUNCTION_CALL edges, the confidence is the lower of the minimum confidence along the path from the definition to the call, and the confidence of the definition statement itself.

For FUNCTION_CALL_RETURN edges, the confidence is always MAYBE, since a function may be called from arbitrary code and we cannot assume where control will return.

Dynamic function definitions

The reaching definitions algorithm does not capture definitions created dynamically inside function calls. Consider the following example:

\cs_new:Nn
  \example_bar:
  { bar }
\cs_new:Nn
  \example_foo:
  {
    \cs_set:Nn
      \example_bar:
      { baz }
  }
\example_foo:
\example_bar:

The final call to \example_bar: should use the redefinition inside \example_foo: (expands to baz), not the original definition on the first three lines (expands to bar). A naive pass would get this wrong.

To handle cases like this, we iterate:

1. Add dynamic edges based on the current reaching definitions.
2. Run reaching definitions again.
3. Replace the old dynamic edges with the new ones.
4. Repeat until nothing changes.

Intuitively, the process converges because each round finishes some calls (their reaching definitions no longer depend on other unfinished calls), and the set of unfinished calls strictly decreases. When no edges change, we have reached a fixed point.

In the above example, both calls start out as unfinished. After the first iteration, the call to \example_foo: finishes, but the call to \example_bar: remains unfinished. After the second iteration, the \example_bar: call also finishes because its reaching definition shifts to the redefinition inside \example_foo:. No unfinished calls remain, no edges change, and the algorithm stabilizes.

Limitations

While the above algorithm works for straightforward expl3 programs, it cannot detect function definitions or calls that arise only through dynamic expansion and are not obvious from the surface text of the program. This limitation is inherent to any static analyzer of a highly dynamic language such as TeX.

While some simple cases may become supported in the future, any attempt to model complex dynamic behavior is constrained both by our incomplete knowledge of the execution environment and by the requirement that the analysis must always terminate in a predictable number of steps.

Get involved!

Your feedback is invaluable. Feel free to contribute or share your thoughts by visiting the project repository. More improvements are on the way as explcheck continues to grow.